Hyperbola
Given 3 points, draw a hyperbola.
Yesterday, I needed to generate the equation for a hyperbola given three points. I still had a spread sheet
from a few years ago when I had to do this, but I did not have any of the derivation. So, I figured I would
write this up nicely and put this on the web.
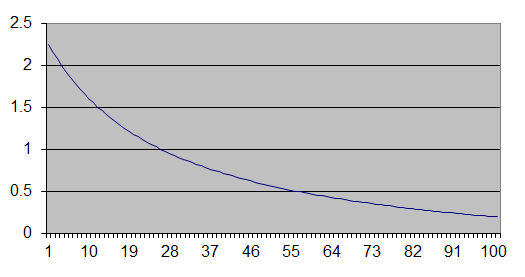
For example, what is the equation of a hyperbola that passes through the points (25,1), (55,0.5), and (165,0)
where the equation is of the form Y=A/(X-B)+C?
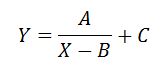
The equation Y=A/(X-B)+C can be worked into the following form.
|
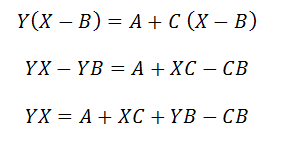 |
|
This form of the equation is a little easier to work with when solving three equations with three unknown.
We will use Alpha for our X values and Beta for your Y values. Here are the three equations we will use.
|
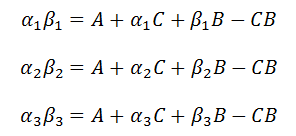 |
|
I observe that it is easy to eliminate the variable A. So, I take the first two equations and subtract.
I do the same with the first and third equation.
|
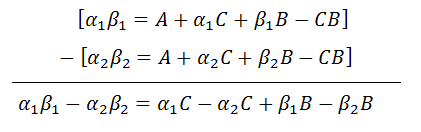
|
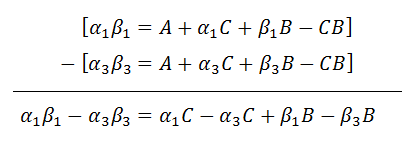 |
|
Each equation can be factored to make it a little more manageable.
|
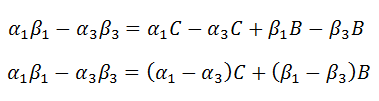
|
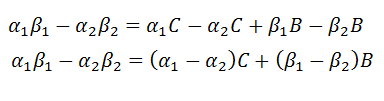 |
|
The two previous equations are in terms of B and C. We use those two equations and eliminate C. (I originally meant to eliminate B so it would look a little nicer...O well!)
I used division to create the common coefficient for the term C.
|
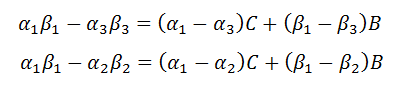
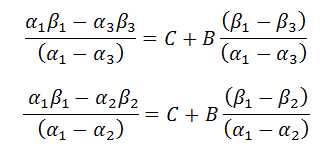
|
|
Now we have a single equation with a single unknown, B.
|
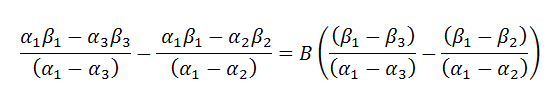
|
|
We will now solve for B.
|
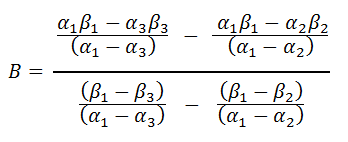
|
|
We can now solve for C.
|
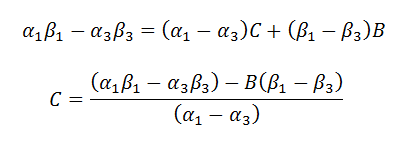
|
|
Finally, we solve for A.
|
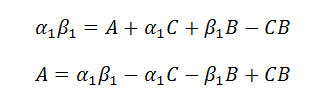
|
|
In summary: The hyperbola of the form Y=A/(X-B)+C that passes through the points (a1,b1), (a2,b2) and (a3,b3), has values for A, B and C as follows:
|
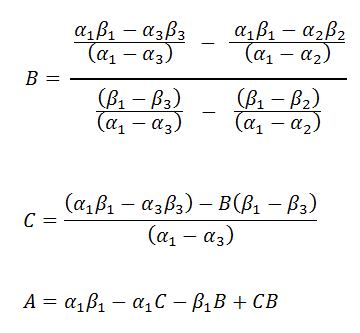
|
|