Speed of a Piston
Speed of a Piston
We hear a lot about how fast a car travels, but most of us rarely
consider how fast the piston travels. This is basically a
math problem. The effect of the connecting rod is a significant factor
that is often under appreciated.
I wrote the first version of this page in 2003. I received many complements
and criticisms. In this rework of the page, I will try to clarify
some of these concepts.
Equations:
|
I first represent the rotation of the crankshaft as a circle
where the center of the circle would be the axis of the
crankshaft and the circumference represents the rotation
of the center of the journal. The piston rod is then
represented as a straight line. Since the piston and the
top of the piston rod travel the same vertical velocity,
the piston itself is not a factor. Figure 1 shows this
representation.
Next, I derived an equation to calculate the location of
the piston. I ignore the piston itself and analyze the
speed of the point where the piston and connecting rod
meet. This point travels the same distance and speed as
the piston.
In this equation I relate the following variables:
- The length of the piston rod
- The radius of the crankshaft. (half of the stroke)
- The angle of the crankshaft.
(I measured this relative to the vertical to help simplify the equations.)
|
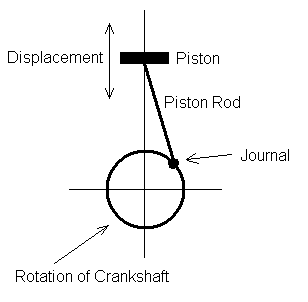Figure 1
|
This relationship was straight forward by using the Law of Cosines.
Then I solved for location using the quadratic formula.
The result can then be simplified by a little Trigonometry.
|
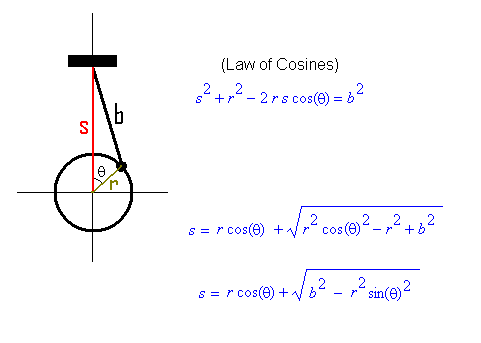
| Figure 2 |
To derive values based on time instead of the angle, I
substitute a function of time for the angle. This relation
is demonstrated in the following table:
| RPM |
|
degrees/second |
|
radians/second |
| 1 revolution/second |
=> |
360 degrees/second |
=> |
2 π radians/second |
| 10 revolutions/second |
=> |
10 * 360 degrees/second |
=> |
10 * 2 π radians/second |
| 100 revolutions/second |
=> |
100 * 360 degrees/second |
=> |
100 * 2 π radians/second |
| ω revolutions/second |
=> |
ω * 360 degrees/second |
=> |
ω * 2 π radians/second |
| Table 1 |
From this data we can establish the relationship between revolutions
per second and radians per second. Making a leap forward,
we can calculate the number of radians traveled by the crankshaft
by multiplying the ω * 2 π radians/second by the number of
second. Thus we have, θ(t) =2πωt. By substituting
this function as our angle
in the displacement equation, s(θ), we
then have the displacement as a function of time.
|
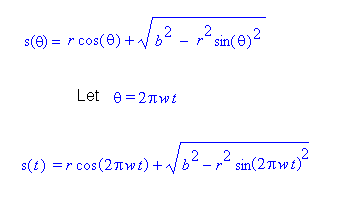
| Figure 3 |
This is probably also a good time to reveal one of my biggest assumptions.
I assume that the rotational speed of the crank is constant when the
engine is held at a constant RPM.
Let's assume the car is in gear and moving at a constant speed. Each piston is
connected to the crankshaft. The crankshaft is connected to the flywheel.
Then we have the transmission, differential unit and
wheels. If the rotational speed of the crankshaft changed as a result of each
piston firing, the vehicle would jerk on each down stroke. All the
connections from the flywheel to the car itself would dampen the effect
of combustion.
The next step is to take the first and second derivative of the location
equation to obtain an equation for velocity and acceleration respectively.
The derivatives of the displacement equation were derived using a
wonderful program called maple.
The graphs and equations shown here are derived from images produced with
maple.
|
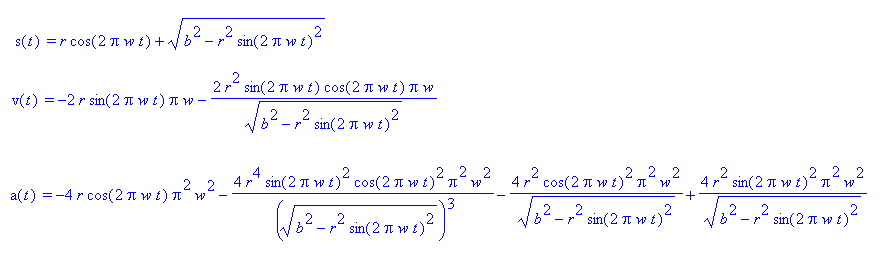
| Figure 4 |
Example:
Now let's use some numbers for these equations and generate some graphs.
I am going to use the radius of 3.5 inches and the piston rod length
of 5.5 inches. The engine will operate at 6000 RPM. These are fictitious
values; however, they demonstrate an interesting aspect of the equations.
Convert RPM to a time interval
Given that the revolutions per minute are 6000, then the duration of
one revolution is 1/6000th of a minute. This implies that one period
of the displacement graph is between t=0 and t=1/6000 minutes.
Let's convert t=1/6000 minutes to seconds:
t = (1/6000)*60 = 0.01 seconds.
So our time interval is from t=0 to t=0.01 seconds.
Let's also convert Revolutions per Minute to Revolutions per Second:
6000 Revolutions/Minute = 6000/60 Revolutions/Second. So 6000 RPM = 100 RPS.
Graph the equations
Given that the revolutions per minute are 6000, then the duration of
Graph 1 is our location equation, s(t).
| r=3.5 inches, b=5.5 inches, ω=100 RPS (6000 RPM) |
 |
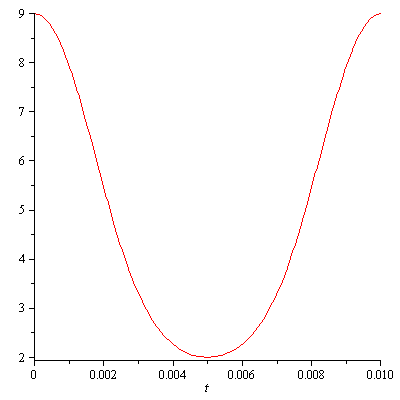| Graph 1 |
We can see that the displacement ranges from 9 inches down to 2 inches.
The 9 comes from 3.5 + 5.5 (radius + rod length) at θ=0 and 2π radians
(360°). The 2 comes from 5.5-3.5 (rod length - radius) at π radians
(180°)
The velocity graph is a little more interesting. I would have expected more
symmetry in this graph. The graph of the velocity as the piston travels up is
not symmetrical to the graph of velocity as the piston travels down. We will
come back to the maximum velocity after the acceleration graph is examined.
|
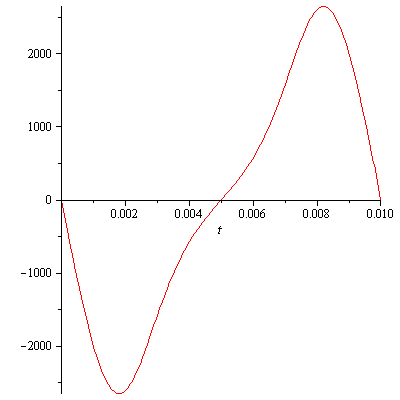
| Graph 2 |
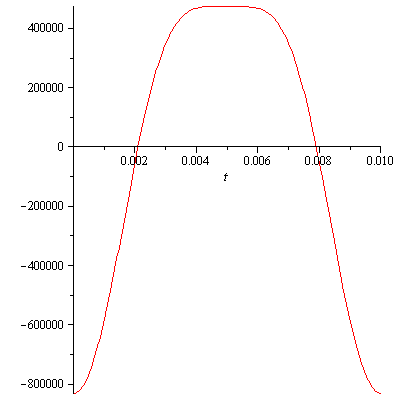
The acceleration graph is by far the most interesting. I thought this was
going to be some simple problem with just some simple sin wave. But,
this graph shows that there is nothing simple about the piston's motion.
|
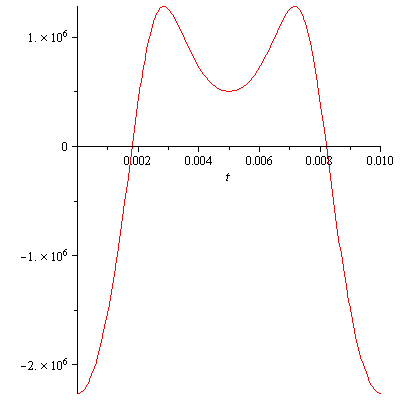
| Graph 3 |
From Calculus we know that the maximum and minimum velocity occur when
the acceleration is zero. The acceleration graph crosses the x-axis at
t=0.001799756496 seconds and t=0.008200243504 seconds.
So what is the answer?
So, back to our original question, "How fast is the piston traveling?"
The velocity of the piston comes out to be
| v(0.001799756496) | = | -2649.246303 inches/second | Moving down |
| v(0.008200243504) | = | 2649.246302 inches/second | Moving up |
This number doesn't mean much to me, so let's convert this to miles per hour.
2649.246302 inches/second
* (1 mile / 63360 inches)
* (60 seconds / 1 minute)
* (60 minutes / 1 hour)
= 151 miles / hour
The astonishing part is that the piston goes from 0 to 151 MPH in 0.0018 seconds!
What is the location of the piston and angle of the crankshaft?
I was also curious at the location the piston when at it's maximum speed.
We can evaluate the location equation for t=0.0018 seconds.
s(0.0018) = 5.99 inches
This means that the piston came from 9 inches down to 5.99 to reach its
maximum velocity. The angle of the crankshaft is found by
converting 2πωt to degrees.
- t=0.0018
- ω=100 revolutions/second (6000 RPM)
- θ = 2πωt = 2π(100)(0.0018)=1.13 radians
1.13 radians * 360°/2π = 64.8°
Notice that this speed is not attained at 90°.
Real Examples
The dimensions in the above example are not realistic, but that example clear
shows the character possible in the acceleration curve. Here are some
realistic examples and the graph of their acceleration.
|
Small Block
|
Acceleration Graph
|
|
| Rod | 5.7 | b = 5.7 |
| Stroke | 3.48 | r = 3.48/2 = 1.74 |
For 6000 RPM a(t)=0 at
t=0.00206 seconds (0.002064150767 sec)
t=0.00794 seconds (0.007935849233 sec)
s(0) = 7.44 inches
s(0.00206) = 5.924 inches
|v(0.00206)| = 1143 inches/second = 65 MPH.
0 to 65 in 0.00206 seconds!
Angle=74.2°
|
|
|
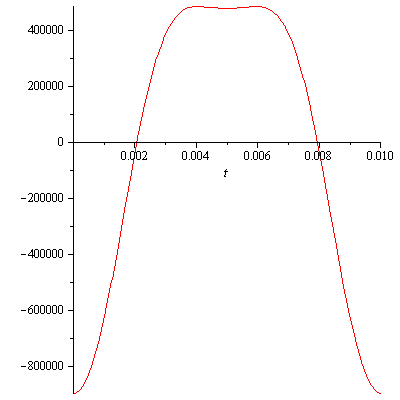
Big Block
|
Acceleration Graph
|
|
| Rod | 6.535 | b = 6.535 |
| Stroke | 4.50 | r = 4.50/2 = 2.25 |
For 6000 RPM a(t)=0 at
t=0.00202 seconds (0.002020804552 sec)
t=0.00798 seconds (0.007979195448 sec)
s(0) = 8.785 inches
s(0.00202) = 6.84 inches
|v(0.00202)| = 1496 inches/second = 85 MPH.
0 to 85 in 0.00202 seconds
Angle=72.7°
|
|
|
Honda S2000
|
Acceleration Graph
|
|
| Rod | 6.024 | b = 6.024 |
| Stroke | 3.307 | r = 3.307/2 = 1.6535 |
| Reported by Jim Knapp |
For 6000 RPM a(t)=0 at
t=0.0021 seconds (0.002100653404 sec)
t=0.0079 seconds (0.007899346596
sec)
s(0) = 7.68 inches
s(0.0021) = 6.218 inches
|v(0.0021)| = 1078 inches/second = 61 MPH.
0 to 61 in 0.0021 seconds
Angle=75.6°
|
|
|
